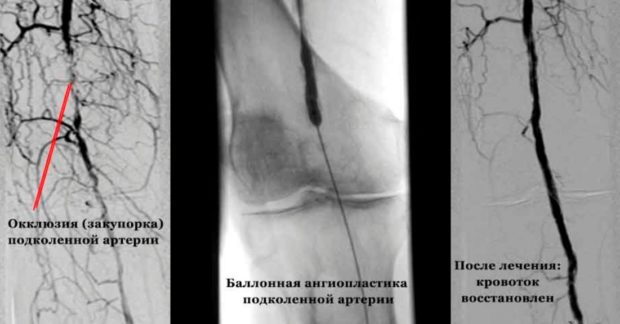
При атеросклерозе критическое число рейнольдса равно 1160

Совокупность методов измерения вязкости жидкости называется вискозиметрией. Прибор для измерения вязкости называется вискозиметром. В зависимости от метода измерения вязкости используют следующие типы вискозиметров.

1. Капиллярный вискозиметр Оствальда основан на использовании формулы Пуазейля. Вязкость определяется по результату измерения времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном перепаде давлений.

2. Медицинский вискозиметр Гесса с двумя капиллярами, в которых движутся две жидкости (например, дистиллированная вода и кровь). Вязкость одной жидкости должна быть известна. Учитывая, что перемещение жидкостей за одно и то же время обратно пропорционально их вязкости, вычисляют вязкость второй жидкости.

3. Вискозиметр, основанный на методе Стокса, согласно которому при движении шарика радиуса R в жидкости с вязкостью η при небольшой скорости v сила сопротивления пропорциональна вязкости этой жидкости: F = 6πηRv (формула Стокса). Эритроциты перемещаются в вязкой жидкости — плазме крови. Так как эритроциты имеют дискообразную форму и оседают в вязкой жидкости, то скорость их оседания (СОЭ) можно определить приближенно по формуле Стокса. О скорости оседания судят по количеству плазмы над осевшими эритроцитами. В норме скорость оседания эритроцитов равна: 7-12 мм/ч для женщин и 3-9 мм/ч для мужчин.

4. Вискозиметр ротационный (рис. 8.12) состоит из двух коаксиальных (соосных) цилиндров. Радиус внутреннего цилиндра — R, радиус внешнего цилиндра — R+ΔR (ΔR << R). Пространство между цилин-

Рис. 8.12.Ротационный вискозиметр (сечения вдоль и перпендикулярно оси)

драми заполняют исследуемой жидкостью до некоторой высоты h. Затем внутренний цилиндр приводят во вращение, прикладывая определенный момент сил М, и измеряют установившуюся частоту вращения ν.

Вязкость жидкости вычисляют по формуле

Применяя ротационный вискозиметр, можно измерять вязкость при разных угловых скоростях вращения ротора. Данный метод позволяет установить зависимость между вязкостью и градиентом скорости, что важно для неньютоновских жидкостей.

Основные понятия и формулы

Окончание таблицы

Задачи

1.Вывести формулу для определения вязкости ротационным вискозиметром. Дано: R, ΔR, h, ν,M.

2.Определить время протекания крови через капилляр вискозиметра, если вода протекает через него за 10 с. Объемы воды и крови одинаковы. Плотность воды и крови равны p1 = 1 г/см3, ρ2 = 1,06 г/см3. Вязкость крови относительно воды равна 5 (η2/η1 = 5).

3.Допустим, что в двух кровеносных сосудах градиент давления одинаков, а поток крови (объемный расход) во втором сосуде на 80% меньше, чем в первом. Найти отношение их диаметров.

4.Какова должна быть разность давлений АР на концах капилляра радиуса r = 1 мм и длины L = 10 см, чтобы за время t = 5 с через него можно было пропустить объем V = 1 см3 воды (коэффициент вязкости η1 = 10-3 Пас) или глицерина (η2 = 0,85 Пас)?

5.Падение давления в кровеносном сосуде длины L = 55 мм и радиуса r = 1,5 мм равно 365 Па. Определить, сколько миллилитров крови протекает через сосуд за 1 минуту. Коэффициент вязкости крови η = 4,5 мПа-с.

6.При атеросклерозе, вследствие образования бляшек на стенках сосуда, критическое значение числа Рейнольдса может снизиться до 1160. Определить для этого случая скорость, при которой возможен переход ламинарного течения крови в турбулентное в сосуде диаметром 2,5 мм. Плотность крови равна ρ = 1050 кг/м3, вязкость крови равна η = 5х10-3 Пас.

7.Средняя скорость крови в аорте радиусом 1 см равна 30 см/с. Выяснить, является ли данное течение ламинарным? Плотность крови ρ = 1,05х103 кг/м3.

η = 4х10-3 Па-с; Rекр = 2300.

8. При большой физической нагрузке скорость кровотока иногда увеличивается вдвое. Пользуясь данными примера задачи (7), определить характер течения в этом случае.

Решение

Re = 2×1575 = 3150. Течение турбулентное.

Ответ: число Рейнольдса больше критического значения, поэтому течение может стать турбулентным.

9. Рассчитать число Рейнольдса для течения крови в капилляре, если скорость течения равна 0,5 мм/с, а диаметр капилляра 0,1 мм. Плотность крови ρ = 1050 кг/м3, η = 4×10-3 Па-с.

10.Определить максимальную массу крови, которая может пройти за 1 с через аорту при сохранении ламинарного характера течения. Диаметр аорты D = 2 см, вязкость крови η = 4×10-3 Па-с.

11.Определить максимальную объемную скорость протекания жидкости по игле шприца с внутренним диаметром D = 0,3 мм, при которой сохраняется ламинарный характер течения.

12.Найти объемную скорость жидкости в игле шприца. Плотность жидкости — ρ; ее вязкость — η; диаметр и длина иглы D и L соответственно; сила, действующая на поршень, — F; площадь поршня — S.

Интегрируя по r, получим:

Пусть поршень шприца движется под действием силы F со скоростью u. Тогда мощность внешней силы NF = Fu.

Суммарная работа всех сил равна изменению кинетической энергии. Следовательно,

Подставив найденное значениеAP во второе уравнение, получим все интересующие нас величины: скорость поршня и, объемную скорость кровотока Q, скорость жидкости в игле v.

Принцип относительности Галилея[править | править вики-текст]

Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, то есть , то ускорение тела относительно обеих систем отсчета одинаково.

Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль (см.второй закон Ньютона), то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-либо конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна

Иным образом этот принцип формулируется (следуя Галилею) так:

Если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.

Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, во многом следует форма и структура ньютоновской механики (и исторически также они оказали существенное влияние на ее формулировку). Говоря же несколько более формально, они накладывают на структуру механики ограничения, достаточно существенно влияющие на ее возможные формулировки, исторически весьма сильно способствовавшие ее оформлению.

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |

Источник

Вязкость (внутреннее трение) жидкости — свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой. Движение реальной жидкости при малых скоростях носит слоистый (ламинарный) характер. При установившемся ламинарном течении бесконечно малые слои жидкости скользят относительно друг друга, не перемешиваясь, и сохраняют во времени свои пространственные положения. При возрастании различия в скоростях соприкасающихся слоёв, силы трения между ними также возрастают. Это приводит к тому, что при некоторой критической величине скоростей, разной для разных жидкостей, характер течения существенно меняется. Возникает энергичное перемешивание слоёв жидкости. Положение слоёв в пространстве с течением времени постоянно меняется, появляются вихри. Такое движение называется турбулентным. Важным свойством турбулентного течения (в сравнении с ламинарным) является высокое сопротивление потоку.

Гидравлическое сопротивление

Чтобы изучить явление гидравлического сопротивления, используем формулу Пуазейля. С учётом объёмного потока жидкости , протекающей через горизонтальную трубу за 1с, формула Пуазейля принимает следующий вид: , где Р1- давление в начале изучаемого участка трубы, Р2 — давление в конце этого участка, l — длина изучаемого участка трубы, η — динамическая вязкость жидкости, протекающей по трубе.

Здесь величина — это гидравлическое сопротивление, как видно оно зависит от радиуса трубы (R), длины участка трубы (l) и вязкости жидкости (η). Гидравлическое сопротивление тем больше, чем больше вязкость и длина трубы и чем меньше площадь поперечного сечения.

Формулу для объёмного потока жидкости можно записать так:

Число Рейнольдса

Характер течения жидкости по трубе зависит от свойств жидкости, скорости ее течения, размеров трубы. Английский физик и инженер Осборн Рейнольдс (1842-1912) изучал переход от ламинарной формы течения к турбулентной. Он экспериментально показал, что турбулентность возникает, когда определенная комбинация величин, характеризующих движение, превосходит некоторое критическое значение. Им было введено безразмерное число, позднее названное в его честь числом Рейнольдса, которое характеризует течение жидкости по трубе (каналу).Число Рейнольдса определяется по формуле: , где ρж — плотность жидкости, η — ее вязкость, V — скорость течения, D — диаметр трубы. Это число является критерием вида течения. Существует критическое значение числа Рейнольдса: для гладких цилиндрических труб ReKp = 2300. Если число Рейнольдса больше критического, то движение жидкости турбулентное, если меньше, то ламинарное. Например, при атеросклерозе критическое число Рейнольдса в некоторых сосудах становится равным 1160.

Так как число Рейнольдса зависит от вязкости и плотности жидкости, то удобно использовать в этой формуле кинематическую вязкость: . Тогда число Рейнольдса можно записать в виде . Число Рейнольдса является критерием подобия. При моделировании гидро- и аэродинамических систем, в частности кровеносной системы, модель должна иметь такое же число Рейнольдса, как и сам объект, в противном случае не будет соответствия между ними.

Кинематическая вязкость полнее, чем динамическая, учитывает влияние внутреннего трения на характер течения жидкости или газа. Так, динамическая вязкость воды приблизительно в 100 раз больше, чем воздуха (при 0°С), но кинематическая вязкость воды в 10 раз меньше, чем воздуха, и поэтому кинематическая вязкость сильнее влияет на характер течения воздуха, чем воды.

Характер течения жидкости или газа существенно зависит от размеров трубы. В широких трубах даже при сравнительно небольших скоростях может возникнуть турбулентное движение. Так, например, в трубке диаметром 2 мм течение воды становится турбулентным при скорости более 127 см/с, а в трубе диаметром 2 см — уже при скорости примерно 12 см/с (температура . 16°С). Течение крови по такой трубе стало бы турбулентным при скорости 50 см/с, но практически в кровеносных сосудах диаметром 2 см турбулентное течение возникает даже при меньшей скорости.

Течение крови в артериях в норме является ламинарным, небольшая турбулентность возникает вблизи клапанов. При патологии, когда вязкость бывает меньше нормы, число Рейнольдса может превышать критическое значение и движение станет турбулентным. Турбулентное течение связано с дополнительной затратой энергии при движении жидкости, что в случае крови приводит к добавочной работе сердца.

Шум, возникающий при турбулентном течении крови, может быть использован для диагностирования заболеваний. Этот шум прослушивают на плечевой артерии при измерении давления крови методом звуков Короткова. Течение воздуха в носовой полости в норме ламинарное. Однако при воспалении или каких-либо других отклонениях от нормы оно может стать турбулентным, что повлечет дополнительную работу дыхательных мышц.

Переход от ламинарной формы течения к турбулентной происходит не только при течении в трубе (канале), он характерен почти для всех течений вязкой жидкости. В частности, обтекание жидкостью профиля корабля или подводной лодки, тела рыбы или крыла самолета или птицы также характеризуется ламинарно-турбулентным переходом, при этом в формулу нужно подставить характерный размер обтекаемого тела и константу, зависящую от формы тела.

Медицинский вискозиметр (вискозиметр Гесса) используется для определения вязкости крови. Принцип его действия основан на том, что скорости продвижения жидкостей в капиллярах с одинаковыми сечениями при равных температурах и давлениях зависят от вязкости этих жидкостей.

Из формулы Пуазейля следует, что объемы жидкостей, протекающих за равные промежутки времени по одинаковым капиллярам, обратно пропорциональны вязкостям этих жидкостей. Следовательно,

Медицинский вискозиметр состоит из двух одинаковых градуированных

капилляров А1 и А2 . В капилляр А2 набирают определенный объем

дистиллированной воды и перекрывают кран Б. Это позволяет

набрать в капилляр А1 исследуемую жидкость, не изменяя уровень воды. Если

теперь, открыв кран Б, создать разрежение в вискозиметре, то перемещения

жидкостей за одно и то же время будут обратно пропорциональны их вязкости

где ηкр — вязкость крови; ηН2О — вязкость воды. Если вязкость воды принять равной единице, а путь, пройденный кровью, составляет одно деление вискозиметра, то на основании формулы относительная вязкость крови численно равна пути lН2О, пройденному при этом водой.

Вязкость крови человека в норме 4 — 5 мПа·с, при патологии колеблется от 1,7 — 22,9 мПа·с, что сказывается на скорости оседания эритроцитов (СОЭ). Венозная кровь обладает несколько большей вязкостью, чем артериальная. При тяжелой физической работе увеличивается вязкость крови. Некоторые инфекционные заболевания увеличивают вязкость, другие же, например брюшной тиф и туберкулез, — уменьшают.

Дата добавления: 2016-07-29; просмотров: 2541 | Нарушение авторских прав | Изречения для студентов